Author: Aboromi Saleh

1. ABSTRACT

Purpose: This study examines the preferences of elementary school students in using inductive considerations when given arithmetic claims, and when they review inductive reasoning as a mathematical proof to an arithmetic claim, as well as teachers' attitudes toward types of reasoning.
Methodology: A survey in which participated 267 pupils from the Arabic sector in three different elementary schools in Israel, in grades 4 to 6. The survey, based on the math reasoning tasks by Healy and Hoils (1998), is comprised of Algebra and Geometry reasoning tasks. Alongside the task, a semi-constructed interview was administered to 12 math teachers in these schools.
Results: The study findings support the research hypotheses that (a) There will be a difference in the students' preferences towards the types of thinking, between grades 4 and 6; (b) Sixth graders will be less likely to accept tautologic and inductive reasoning than fourth graders; (c) Elementary school pupils tend to prefer empirical arguments (such as inductive and example) as their approach rather than the arguments that they believe will receive the highest scores from their teachers. However, findings do not support the hypothesis that there will be a difference in teachers' preferences towards different types of thinking. The research findings and their practical implications are discussed together with recommendations for teachers and educators in the field of mathematics and teacher training.

2. INTRODUCTION

While studying mathematics at school, pupils are often required to formulate and test assumptions, to explain and justify conclusions and to prove general theorem or claims. The proof is the mathematical tool through which, by argumentation, the correctness of a mathematical claim is established and given universal validation, or the opposite confirming that the claim is false thus refuting it (Hanna, 1989). An argumentation comes in order to persuade ourselves and others about the correctness of a hypothesis and consists of a claim and a conclusion. A claim is a statement that the addresser asks the recipient to accept as a truth or a modus operandi, and the addresser must prove it (Toulmin, 1969). Claims refer to the discursive methods of science and include the expression and justification of the claims, observation in opposite attitudes and evidences, and the social negotiation about data and theories (Sadler & Fowler, 2006). A high level of argument expresses a high level of literacy (Glassner & Schwartz, 2001). Students in the elementary schools apply external justification methods, empiric techniques of justification and an analytic justification technique (Flores, 2002). One of the elementary school's curriculum goals is to foster critical thinking skills in students. Critical thinking is a balanced reflective thinking focused on the decision what to believe and how to operate. Developing critical thinking skills is a condition for consuming information and significant processing of it that enables implementing the knowledge. Argumentation skills are part of the critical thinking skills set and constitute preliminary and essential background for activating a process of decision making. Young students can develop mathematical claims of high potential to be called proofs in elementary grades (Stylianides, 2007b). Each time they are asked to reason, explain, validate, claims and make conclusions, we are fostering and optimizing their thinking abilities. Unfortunately, many times, students’ replies to these questions are poor due to a variety of reasons. Some of which originate from the development process of verbal and lingual skills and others stem from cognitive and intellectual development processes, that are age dependent.
The importance of this study is in examining the inductive tendency of elementary school pupils in the Arab sector in Israel, in an effort to shed light on the developmental process of argumentation and reasoning in these ages. This research differs from prior researches in two aspects: first it includes elementary school pupils in grades 4-6, whereas most researches in Israel included only high-school students. Second, it examines students in the Arab sector exclusively, which were not included in prior researches.

3. Literature background

In schools, the status of mathematics today is similar to that of Latin in the 19th century. This profession is considered one of the hardest professions, and one of the most hated of some students. However, mathematic skills are important for all learners in "real" areas, since it is one of the basic tools used in these fields. For example, the quantitative thinking section of the Psychometric Entrance Test in Israel examines mathematical skill and emphasizes the importance of mathematics studies to all those wishing to continue their studies at the university. Most of the mathematical markings used today were invented only in the 16th century. Like musical notes, the modern mathematical lines have a precise and rigid syntax, encoding information that will be difficult to write in any other form. The mathematical language may also be difficult to understand for beginners. Words such as "or" have an accurate, and sometimes different, meaning from the everyday language. In addition, words such as "open" and "field" have acquired special mathematical significance.

Many researchers have referred to the various approaches that deal with the development of early childhood thinking and their implications for mathematical education. The approaches differ in two main dimensions. One is the extent to which the structures and developmental processes are domain-dependent, occurring at a uniform rate in different areas, or occurring at a different pace in different areas, and in the autonomy of the development process-whether it is innate or environment dependent (Dehaene & Cohen, 1995). Piaget (1965) argues that children are not passive to the environment. On the contrary: they check the environment, seek solutions actively, and of course – ask questions. Piaget focused on the cognitive processes of collecting and processing knowledge (rather than the knowledge that children acquire). He compared the development of intelligence to physiological development. Piaget has observed four major stages in cognitive development.

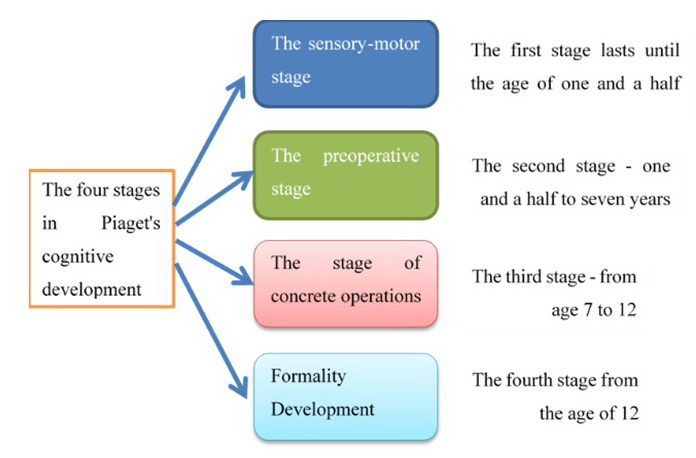
At each stage, children acquire new intellectual skills based on the previous stages:
It should be pointed out that although the stage sequence is fixed, each individual has his or her own pace. There are also interpersonal and intercultural differences during each stage. Piaget argued that our ability to think develops with age and is the result of interaction with the environment. The connection between the environment and the child triggers stimuli all the time, the response to these stimuli leads to learning. Therefore, in order for the child to achieve the acquisition of a mathematical concept such as "proof," he must first understand what it is to prove, or know how to correctly explain things that are based on the concept and as long as these skills are not acquired he has not reached the appropriate stage in the development of thinking, Some mathematician. This approach is called constructivist and sees learning as a process of knowledge-building through independent inquiry conducted in interaction between the child and the environment.
I focus on the third and fourth stages, and the development of the proof at this stage, and the students' tendency to explain things inductive form. The stage of concrete operations takes place during elementary school, at the age of 7-12. As is well known, at this age, thinking is no longer intuitive or egocentric, as it was during the preschool period. This stage is characterized by logical thinking, which allows for legality, reasoning through logical rules, and so forth. Their judgment and judgment are based on reasoning. Some students are able to perform logical actions only in situations involving concrete, tangible objects. And there are those who have the ability to understand through symbolic or verbal examples. Such students still need illustrations through examples. The fourth stage is the most advanced stage in which intellectual development reaches a peak characterized by deductive thinking. A person at this stage can acquire knowledge and use it in the most efficient manner. According to Piaget, the child is gradually released from the grasp of concrete thinking and acquires the ability of abstract thought. Transition from a thinking style is based on the ability to think beyond the tangible. It is therefore possible to utilize the abilities of students who have formal thinking. However, they need concrete or inductive examples to illustrate the situation of a given argument, or before they understand or attack proof that they will have to make inductive inferences. I suggest here that there is a transition stage between the third and fourth stages, or there is room for dividing the two stages (third and fourth) into two parts: third stage, first part, simple concrete operations, and two complex concrete operations.

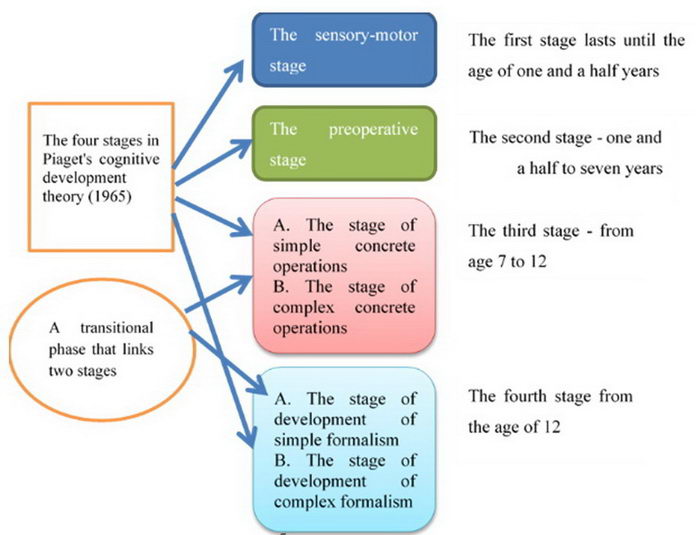
And a fourth, a low deductive first part, and a second deductive part. In other words, I suggest that the student, in order to move from the concrete stage to the formal thinking stage, will be in an intermediate stage that will connect the two stages, which I will call a low deductive stage.
Cultivating thinking is a primary goal in all educational institutions and curricula. According to this, every teacher must be aware of how the learner's thinking is being promoted. But this is not a sufficient condition in the classroom situation in a school, "Teacher awareness of the need to advance thinking is a prerequisite for the existence of a challenging and interesting learning process, but the question is whether it is also a Satisfactory condition" (Zohar, 1996, p. 4). Swartz offers the concept of stimulating and stimulating learning in the context of high-order thinking. This learning is based on the constructivist approach of developing a deep understanding of a meaningful subject for the learner. This understanding is achieved through problem solving authenticity, during which an emphasis is placed on building the learner's knowledge in a thinking community and developing a self-directed and metacognitive and reflective learner (Swartz, 2008). Meta-cognitive intuitive thinking that develops in the early school years is very basic, and only becomes complex and linked to learning processes when learning incorporates explicit use of metacognitive components. Metacognitive skills first develop in separate content domains, and only in explicit conceptualization and inclusion processes may move beyond different content domains in the "main way" of transference (Salomon & Perkins, 1989). Most researchers have put a lot of emphasis on the need for developing argumentation and discussion skills among students. Means & Voss (1996) proposed making learning an argument as a basis for informal reasoning learning, and this would be a separate content area to be taught in schools Duschl (2008). However, even teachers who combine argumentative skills promotion rarely do so (Newton, Driver & Osborn, 1999).
For the purposes of this study proof is seen as a process of (A) determining truthfulness of mathematical statements and arguments and validating or refuting them through the construction of mathematical meanings that have individuality and social aspects, the same as Harel and Soder (1998) who combine examination and persuasion; and (b) the transfer of these meanings through arguments as described by Stylianides (2007), by means of groups of conventional statements, modes of argument, and methods of representing a common argument in a society or group or class, that is proof is the product of the process of justification and validation accepted by the community is in a classroom or group or company. Marten & Harel (1989) indicated the difficulty of teachers’ understanding the proof essence, and that elementary teachers accept inductive claims as proofs, also, they did not reject “proofs” that were false, but indicated in a deductive way (Marten & Harel, 1989; Goetting, 1995) similar researches that referred to teachers in high schools showed that similar findings also (for example, Knuth, 2002). Ball, Lubienski and Mewborn (2001). They indicated teachers’ poor understanding of the proof nature, such as their tendency to accept empiric claims (namely, examples) as sufficient to base the correctness of a claim.
Many researchers have pointed to the students' difficulty in tracking and building mathematical proofs (Healy & Hoyles, 2000; Fischbein, 1982; Stylianides & Stylianides, 2009), the students face difficulties in understanding mathematical evidence, and do not distinguish between inductive-empirical evidence and formal-productive evidence and their use to draw conclusions and build new knowledge. Many studies have found that there is an inductive tendency among students of different ages. The reason for this tendency is everyday life; Anderson (1985) calls everyday proofs as "inductive valid arguments" and explains that people create and examine assumptions based on their likelihood, and refute and attack these assumptions according to their own experience. There are hierarchical stages, which are defined in the development of the understanding of formal proof, and the inductive stages are the first ones; moreover, Van Dormolen (1977) proposed a hierarchical model that includes three developmental stages of the concept of formal proof: first, the student uses an example to obtain a sense of a given argument. In the second stage he tries several other examples, and examines the common characteristics of all the examples of the claim. A third stage is the stage in which the student attempts to obtain formal proof. Then we see that the first two stages are inductive and the third is deductive. The purpose of this study is to examine the development of acquiring the concept of proof and critical thinking among elementary school students.

4. Methodology

4.1. Sample
This research is based on three studies, held in three Arabic sector schools in Israel. Study 1 is a quantitive study, in which 267 pupils in grades 4 to 6 in elementary schools in the Arab society participated. Study 2 is a qualitative study which included 12 teachers of the pupils in study 1. Study 3 contains further statistical analysis designed to test the validity of a scheme that describes the evolution of thinking (picture #). All three schools are in the same socio-economic measure. All pupils who participated in this research come from heterogenic groups of all levels.
4.2. Study 1
Research procedure
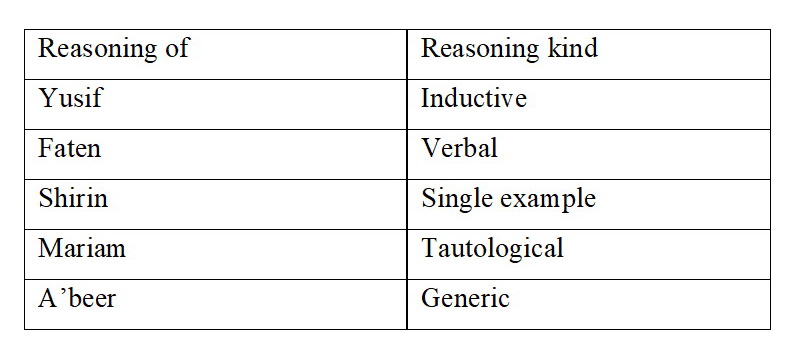
In this research I focus on the way pupils refer to two types of claims: (A) Arithmetic claims: "the sum of each two even numbers is even" and "the sum of each two odd numbers is odd" and (B) Geometric claims: "the sum of interior angles of each triangle is 180 degrees" and "the sum of each quadrate is 360 degrees". For this purpose, pupils were asked to respond to math reasoning tasks presenting different kinds of reasoning, according to the math reasoning tasks by Healy and Hoils (1998) which include correct and false reasoning of the two claims mentioned above. Each pupil completed two tasks: one in algebra and another in geometry and were asked in each task to determine according to their opinion, concerning each presented argumentation whether it is correct or not. All the reasoning and argumentation is either explained by inductive numeric examples, verbal generalizations, generic everyday reasoning or tautological reason.

4.3. Research tools
The research tool is a closed math reasoning task in Algebra and in Geometry. It was found that the reliability level (Alpha Cronbach) of all items and all variables is higher than 0.9. the task detailing according to reasoning kind is as follows:
4.4. Study 2: Teachers interviews
After pupils completed the tasks in study 1, their teachers were interviewed in a semi-structured interview about the same algebraic and geometric claims. The purpose of the interview in this study, is to complete the picture by adding teachers views and preferences regarding students' reasoning preferences, arising from questions such as: What are the attitudes of teachers regarding mathematical questions that require proof? Which reasoning styles are preferred by teachers?
What do teachers know about students' preferences for reasoning styles? Teachers' answers underwent a process of content extraction for key ideas and textual motifs that were later-on processed into central themes in the qualitative analysis of teachers' attitudes and preferences regarding reasoning methods and proof of mathematical arguments. It was expected that in light of the developmental process of mathematical thinking over the years, there will be a difference between the preferences of adults and the types of reasoning for mathematical arguments, especially when it comes to mathematics teachers. However, as far as the ways of explaining math arguments in a classroom are concerned, teachers would be aware of the students' need for concretization and examples in accordance with the mathematical thinking development process.

4.5. Study 3: further analysis of open-ended questions
In this study, teachers in each classroom first explained to students, two claims. One was a claim in algebra and the other was a claim in geometry. Following this, students were asked to explain why the argument was correct while reasoning their answer. Students' answers were coded in two scales. The first coding was of type of reason, either it was tautological, single example, inductive, verbal, generic or visual. The second scale was designed to give a quantitve measure of the quality of the students' answer by a single mark. The mark is a cumulative sum of three different marks given as follows:
For example, an answer that contained partial reasoning that is tautological and can be applied only to a single case would get an overall mark of 2+1+1=4. Students' replies were coded and analyzed using one-way Anova, in order to investigate whether there is a statistical difference between the marks in different grades. The Chi-square test was conducted to compare whether there is a statistical difference in the type of reasoning between the three grades.
5.9. Research hypotheses
(A) There will be a difference in the students' preferences towards the types of thinking, between grades 4, 5 and 6.
(B) Sixth graders will be less likely to accept tautologic and more inductive thinking than fifth and fourth graders.
(C) Elementary school students tend to prefer empirical arguments (such as inductive and example) as their approach rather than the arguments that they believe will be the highest scores.
(D) There will be a difference in teachers' preferences towards different types of thinking.
(E) Primary teachers will disapprove of empirical arguments (eg, inductive and example), and will not give these reasons the highest scores.

5. Results

5.1. Descriptive statistics
The survey was administrated to 244 pupils in algebra and to 267 pupils in geometry. In algebra the sample was made of 119 boys and 125 girls; there were 83 pupils in the 4th grade, 81 in the 5th grade and 80 pupils in the 6th grade; 82 pupils in the school Alzahra, 80 pupils in the school Alsalam; 82 pupils in the school Ailut-A. In geometry the sample was made of 126 boys and 141 girls; there were 91 pupils in the 4th grade, 89 in the 5th grade and 87 pupils in the 6th grade. 89 pupils in the school Alzahra, 92 pupils in the school Alsalam; 86 pupils in the school Ailut-A.

5.2. Research hypotheses testing
Testing the hypothesis that there will be a difference in the preferences of pupils toward types of reasoning, between the 4th, the 5th and the 6th grade, a chi-square test was conducted. Supporting the hypothesis, the distribution of reasons was significantly different between the grades in Algebra: χ2(8)=33.874, p<0.001 but not in Geometry (χ2(8)=10.277, p=0.246). Regarding pupils' knowledge about their teachers' preferences, this time a chi-square test was not significantly different between the grades in Algebra: χ2(8)=12.377, p=0.135, as more than 50% of all pupils chose inductive reasoning, but was significant in Geometry (χ2(8)=24.662, p=0.002<0.01).
A difference in domain was indicated as significant differences were found between 4th and 6th grade in Algebra: χ2(2)=29.932, p<0.001 but not in Geometry: χ2(2)=3.932, p=0.08, as well as for 5th and 6th grade, (Algebra: χ2(2)=24.537, p<0.001; Geometry: χ2(2)=2.957, p=0.228.).
In order to test the hypothesis that there would be a difference in the answers of pupils toward A1.1-A1.3 questions, a Friedman test was conducted. Supporting the hypothesis, the distribution of reasons was significantly different between the questions for Algebra: χ2(2)=35.421, p<0.001 as well as for Geometry: χ2(2)=24.632, p<0.001. To test the hypothesis that there would be a difference in the preferences of pupils toward visual type of reasoning, between the 4th and the 6th grade, a chi-square test was conducted. Not supporting the hypothesis, the distribution of answers wasn’t significantly different.

5.2.1. Analysis of the answers to the open question
Most of the explanations given by students as answers to the open question in Geometry, combine visual examples with rectangles or squares. This is very much related to the students' intuition, but the sixth graders often combined more than one representation in their explanation, which indicates more developed thinking. And yet the difference is not great, it can be explained that students have more difficulty in geometry than algebra. Another point is that all the students in their examples drew rectangles and squares horizontally and this is related to the students' visual perception of square shapes in examples and opposite examples. In a similar way, most of the explanations given by students to the question in Algebra used single example or inductive ways of thinking.

5.3. A thematic analysis of teachers' attitudes regarding proofs
A textual qualitative analysis pointed out five main themes, which were subsequently expanded and detailed into the following sub-themes. Depth and complexity – The expressions "depth" and "complexity" versus "simplicity" were used frequently by the teachers. These terms were used in a dual way, both for characterizing students' arguments and for characterizing questions that require proof of "deep" or "complex" questions. Use of examples – The teachers relate to the students' need to use the examples as proof, and the development of the sample level and types of samples according to age. The examples are not only used by students to prove the claims, but also by the teachers, when they teach new material in the classroom or explain a solution of questions. The texts show that examples play an important role in both processes. The teachers' preference for certain arguments versus what they think about their students' preference – The teachers often distinguish between arguments and examples that they would prefer to accept or use, and the arguments or examples that they thought were preferable to the students. Teachers prefer to accept arguments based on definitions of concepts or on a chain of arithmetic operations. This is in contrast to what they think will be preferred to the students, i.e. examples of everyday life and numerical examples. Instrumental value of learning to prove – Throughout all the interviews teachers refer to the learning and teaching of proving as an action that develops thinking, creativity, and creates an analogy to other areas of thought. Teachers perceive these questions as requiring the application of high levels of thinking, because their practice develops students' abilities in mathematics and other fields of study. Elementary school does not teach enough mathematical proof – Teachers mentioned lack of time and curriculum time constraints as reasons for not investing enough in teaching to prove.

5.4. Analysis of the answers to the open question
The Chi-square test was conducted to compare whether there is a statistical difference between grades. A difference was between grades in Algebra: χ2(10)=20.308, p=0.02, as in the sixth grade student use less tautological and single example ways of thinking and use more the verbal way of thinking. The explanation of student and the way of thinking were coded to additional mark that referred to way of thinking and to how corrected it was explained by student. One-way ANOVA test found no difference between grades: F(2)=1.288, p=0.278. A similar result was found in Geometry: χ2(10)=40.474, p>0.001, as sixth grade student use less tautological and visual ways of thinking and use more inductive and verbal ways of thinking. One-way ANOVA test found a difference between grades: F(2)=33.985, p>0.001. An analysis of answers for open questions showed that for geometry the differences between ways of thinking are more significant than for algebra.

5.5. Validation
To validate pupil’s own statement by types of reasoning and score they received in accordance with types of reasoning, two criterions were used – student's total average score and student's math’s score. To check whether there is a difference in student's total average score and student's math’s score between the student's preferences toward types of reasoning and between the 4th, 5th and the 6th grade, two-ways ANOVA tests were conducted. The first ANOVA test examined if there is a difference in the student's total average scores between types of reasoning, and between the grades. The model revealed that there is a significant difference in student's total average score between types of reasoning, and between the grades: F(14,120)=6.504, p<0.001. A main effect for types of reasoning variable was found: F(4,120)=14.233, p<0.001. The post hoc tests revealed that there are significant differences between tautological type of reasoning and between every other type of reasoning, p<0.001 for all cases. The second ANOVA test examined if there is a difference in math’s student grade between types of reasoning, and between the grades. The model revealed that there is a significant difference in math’s student grade between types of reasoning, and between the grades: F(14,120)=6.562, p<0.001. A main effect for types of reasoning variable was found: F(4,120)=17.283, p<0.001. The post hoc tests revealed that there are significant differences between tautological type of reasoning and between every other type of reasoning, p<0.001 for all cases. No significant differences were founded between other types of reasoning.
To check for a statistical correlation between the score students received in accordance with types of reasoning in pupil’s own statement and between student's average score and math score, Pearson correlations were calculated for all grades and for every grade, respectively. The test indicated high power significant Pearson correlations between the score students had in accordance with types of reasoning statement and between student's total average score and for student's math’s score for 4th, 5th and the 6th grade, with some differences between the grades.

6. Discussion

6.1. General
A survey administrated to 267 pupils in three different schools in the Arabic sector in Israel, has been held in order to learn about the preferences of elementary school students toward types of reasoning, in proof type of questions, in Geometry as well as in Algebra. Results of the survey, alongside text analysis of teachers' positions regarding them, reveal a lot on this issue.

6.2. Theoretical implications of the results
The sum total of findings emerging from the empirical chapter of this study indicate differences in the form of reasoning favored by elementary school students as they progress in age. The resulting picture suggests that as students mature, their tendency is to prefer verbal and generic reasoning over tautological and empirical reasoning. These findings were found to be consistent and robust beyond different schools. The basis for a theory that can explain this finding lies in Dewey's (1933) definition of the concept of reflective thinking. This concept comes to explain the process by which new information is created while processing existing information as defined similarly by Bartlett, Lewis and Smith (1993). Furthermore, it can be suggested that there is a cyclical process in which reflective thinking produces new information, and in the process the student develops to a higher level of thinking. At the new level, reflective thinking exists at a higher level of complexity, which allows for the creation of new information based on information learned earlier and so on.
At the same time, this process of proving mathematical arguments itself constitutes a framework of reflective thinking, in which the student is required to apply formal rules and information, in order to create a logical structure that will confirm or refute the given argument. In such a way, in fact, the student creates new information, both about the correctness or refutability of the specific argument, and about how critical logic and thinking tools are used in relation to mathematical arguments. As the process progresses, and when the student reaches the higher levels of thinking, he will be able to apply this method in other areas of knowledge as well. This stage is a stage of reflective thinking by definition (Brown, 1987; Flavel, 1979).
Another theoretical contribution that can be attributed to the present research is the confirmation of Eshet's (2004) claim that high-order thinking can be taught and developed at school. Indeed, exploring the subject of proof-reading in elementary school illustrates this. For example, if we refer to the definition of Passig (2001) that offers some revision to Bloom's taxonomy (1956). One of the high levels of thinking he counts is that of transcription thinking. This level of thinking, to a certain extent, resembles synthesis, in that the learner makes use of formal information that already exists, and the techniques he or she controls and through which new information is produced. For school students, this is the process they need to prove or disprove a mathematical argument. As the findings of the present study teach us, this ability improves between grade to grade, thus supporting the assertion of Eshet (2004).
Finally, a unified conceptual framework of the contribution of the present work to theoretical research in the field can be found in the scheme proposed earlier. This scheme seeks to describe how student's learning experiences and other individual experiences in general influence the development of the set of constituents whose joint action produces the result of formal thinking in a funnel-like configuration. This system, which is based on recurring rounds of feedback and relies on them for improvement, does not necessarily operate linearly and unidirectionally, as I mentioned before, but can even move inversely. A substantial part of Chapter 4 focused on describing and explaining various factors and contributors of math inconsistency in students. These factors include teaching methods, inherent difficulties in math, language and visual components, perception of mathematics as a set of local rules and others. These factors produce inconsistencies in the student which disrupt the assimilation and learning of mathematical concepts and procedures. In addition, the inconsistency adversely affects the development of mathematical intuition in the student. As a result, essential elements within the funnel are compromised, and the respective result may be expressed in the student by showing signs of regression in the level and quality of formal thinking, or at least not seeing the progress expected according to grade or age level. This can also result in the student being treated by means that are not suitable for their needs, frustration for the student, for their environment and teaching staff, and decline in academic achievements. Hence, the importance of teaching lies in its ability to reduce sources of inconsistency, to create positive learning experiences, to empower fundamental skills needed for math literacy, and to strengthen student intuition. In the next subsection, I will make some practical recommendations for teaching staff and other professionals in the field, based on the insights gained within this research.

6.3. Limitations of the study
Several limitations may apply to this study. First, it should be noted that the study was conducted among students from the Arab sector in Israeli schools. This fact can limit the ability to generalize the conclusions of the study. However, it is important to note that the study involved students from three different schools and different layers of society. Second, the test used in this study is presented in a format that the students are not familiar with. On the other hand, it is possible that if the test were presented in a format that is too familiar, there's a risk of ceiling effect. It should also be noted that the test chosen for this study is based on the valid and reliable Math Reasoning Tasks by Healy & Hoils (1998). Furthermore, results of study 3 support the findings obtained using the Healy-Hoils reasoning task (1998) in study 1, as they are based on a different task contribute to the robustness of the findings.

6.4. Conclusion
At the basis of this research stands the assumption that development of critical thinking skills is a necessary condition for learning and processing of new information as well as implementing the knowledge that is derived from it. In the process of critical thinking argumentation skills are a preliminary and essential component. As shown in the schema describing the development of formal thinking in mathematics and in general, there is a process of recurring feedbacks throughout the school years and parallel to the student's psycho-intellectual development stages. This scheme was validated through a thorough examination of the variables using quantitative and qualitative techniques. Its explanatory ability for the phenomenon described is very high, in keeping with the research literature that preceded it and offering solutions to material problems arising from previous writing. The findings of the present study indicate that the process is not as linear and unidirectional as Piaget's theory might suggest. Therefore, the descriptive framework proposed in this study may help to somewhat alleviate the contradiction that a large number of teachers experience between their formal knowledge of students' intellectual development and what they see in practice.

7. Bibliography

1. Anderson, J.A (1985). Cognitive psychology and its implications. New York: W.H freeman.
2. Ball, D. L., Lubienski, S., & Mewborn, D. (2001). Research on teaching mathematics: The unsolved problem of teachers’ mathematical knowledge. In V. Richardson (Ed.), Handbook of research on teaching. (pp. 433-456) New York, NY: Macmillan.
3. Bartlett, F.A. (1932). A Study in Experimental and Social Psychology. New York: Cambridge University Press.
4. Bloom, B.S. (ed.) (1956). Taxonomy of educational objectives: The classification of educational goals: Handbook I, cognitive domain, Longmans, Green, Toronto.
5. Brown, A. (1987). Metacognition, Executive, Control, Self Resolution and other more Mysterious Mechanisms. In F.E. Weinet & R.H. Kluer (Eds), Metacognition. Motivation, and Understanding. Hillsdale, Erlabaum. NY.
6. Dehaene, S. & Cohen, L. (1995). Toward an anatomical and Functional Model of Number processing. Mathematical cognition, 1(1), 83-120.
7. Dewey, J. (1933). How We Think. Boston.
8. Dreyfus, T. (2000). Some views on proofs by teachers and mathematicians. In A. Gagatsis and Gr. Makrides (Eds.), Proceedings of the 2nd Mediterranean Conference on Mathematics Education. (pp. 11-25.) Nicosia, Cyprus: Cyprus Mathematical Society and Cyprus Pedagogical Institute.
9. Duschl, R. (2008) Science Education in Three-Part Harmony: Balancing Conceptual, Epistemic, and Social. Review of Research in Education, 32. 268291.
10. Eshet, Y. (2004). Digital literacy: A Conceptual Framework for Survival Skills in The Digital Era. Journal of Educational Multimedia and Hypermedia, 13 (1) 93-106.
11. Flavel, J. H. (1979). Metacognition and Cognitive Monitoring – A New Era of Cognitive-Developmental Inquiry. American Psychologist, 34, 906-911.
12. Fischbein, E. (1982). Intuition and proof. For the Learning of Mathematics, 3(2), pp. 9-18, 24.
13. Flores, A. (2002). How Do Children Know That What They Learn in Mathematics is True?, Teaching Children Mathematics, 8, pp. 5, 269-274.
14. Goetting, M. M. (1995). The college students’ understanding of mathematical proof University of Maryland: Doctoral dissertation.
15. Healy, L. & Hoyles, C. (2000). A study of proof conceptions in algebra. Journal for Research in Mathematics Education, 31(4), pp. 396-428.
16. Healy, L. and Hoyles, C. (1998) Technical Report on the Nationwide Survey: Justifying and Proving in School Mathematics Institute of Education, University of London.
17. Hanna, G (1989). Proofs that prove and proofs that explain In G Vergnaud, J. Rogalski, & M. Artigue (Eds.), Proceedings of the International Group for the Psychology of Mathematics Education Vol II, (pp. 45-51), Paris.
18. Harel, G. (1998). Two dual assertions: The first on learning and the second on teaching (or vice versa). American Mathematical Monthly, 105, pp. 497–507.
19. Knuth, J. (2002). Secondary School Mathematics Teachers' Conceptions of Proof. Journal for Research in Mathematics Education, Vol. 33, No. 5, pp. 379- 405.
20. Means, M. L., & Voss, J. F. (1996). Who reasons well? Two studies of informal reasoning among children of different grade, ability and knowledge levels. Cognition & Instruction, 14(2), 139-179.
21. Newton, P., Driver, R., & Osborne, J. (1999). The place of argumentation in the pedagogy of school science. International Journal of Science Education, 21(5), 553-576.
22. Piaget, J. (1965). The Child's conception of Number. New York: W.W. Norton & co.
23. Sadler, T. D. & Fowler, S. R. (2006). A threshold model of content knowledge transfer for socioscientific argumentation. Science Education, 90, pp. 986–1004.
24. Salomon, G., & Perkins, D. N. (1989). Rocky roads to transfer: Rethinking mechanisms of a neglected phenomenon. Educational Psychologist, 24(2), 113142.
25. Stylianides, A. J. (2007a). Introducing young children to the role of assumptions in proving. Mathematical Thinking and Learning, 9(4), pp. 361–385.
26. Stylianides, A. J. (2007b). The notion of proof in the context of elementary school mathematics. Educational Studies in Mathematics, 65, pp. 1–20.
27. Stylianides, G. J, & Stylianides, A. J. (2009). Facilitating the transition from empirical arguments to proof. Journal for Research in Mathematics Education, 40, pp. 314-352.
28. Swartz, R. J. (2008). Energining Learning. Educational leadership, 65 (5), 26-31.
29. Swartz, R. J. (2001). Infusing the Teaching of Critical and Creative Thinking into Content Instruction. In A.L Costa (Ed.) Developing minds. Association of Supervision and Curriculum Development (pp. 266–274). Alexandria, Virginia, USA.
30. Van Dormolen, J. (1977). Learning to understand what giving a proof really means. Educational Studies in Mathematics, 8, pp. 27-34.
31. Zohar, A. (1996). Learn, think and learn to think. Jerusalem: Branco Weiss Institute for Cultivation of thinking.